|
1.集合論 ☆☆☆ 現代数学における二つの重要な概念は「集合」と「無限」である。 カントールの対角線論法 仮に実数が番号順に並べられていたとする(背理法)。

小数第1位から少数第無限位まで(←ここが新しい論法!)各位の数字が違う新しい実数を作ると、これは0から1までの実数なのに番号がついていない。だから、実数の集合は番号がつかない。
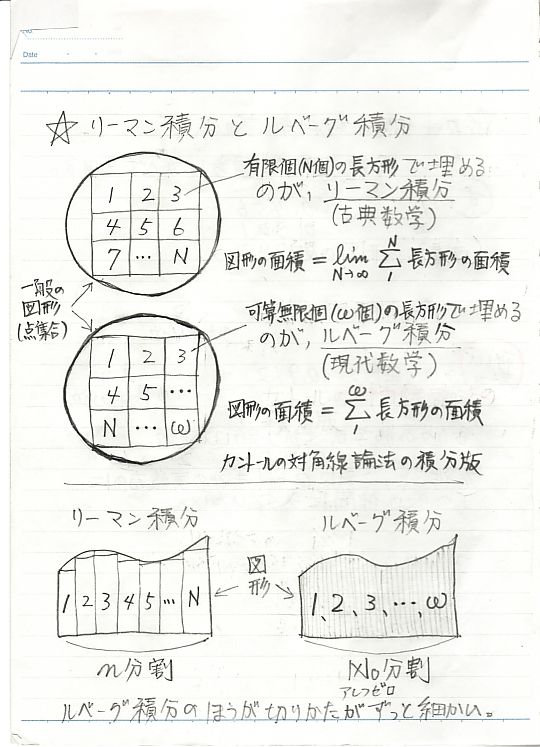



要するに、リーマンは「人間は図形を有限個の長方形に区切り、それら有限個の長方形の面積を足し合わせることしかできない」としたが、ルベーグは「人間が図形を可算無限個(実無限個)の長方形に区切り、それら可算無限個の長方形の面積を足し合わせることができる」としたのだ。リーマンの世界とルベーグの世界とでは、人間に与えられた能力に大きな違いがあるのである。
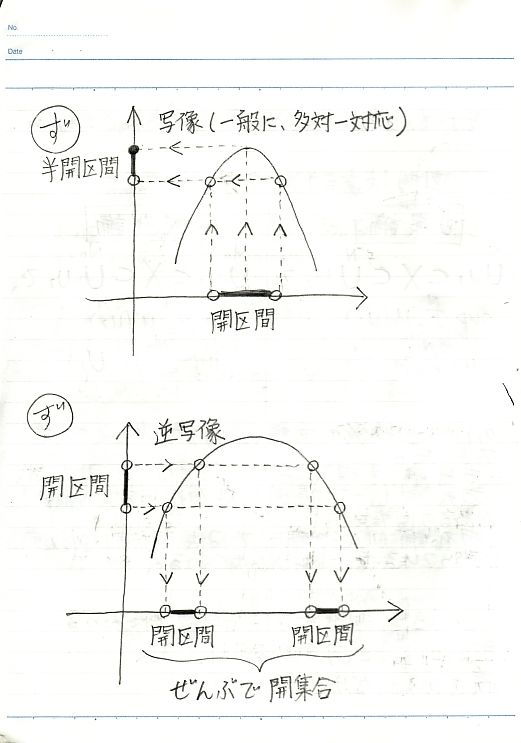
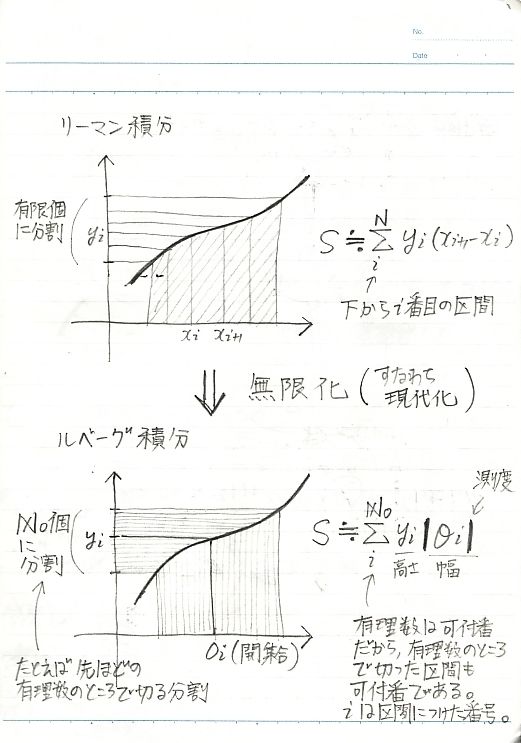
ルベーグ積分を知ったからと言って、ラプラス変換やコーシーの留数定理のように積分の特別な計算法が身につくわけではない。ただ、積分可能な図形の範囲が広がるだけだ。
『どうすれば数学がわかるか?』 ☆☆ h13.12.15
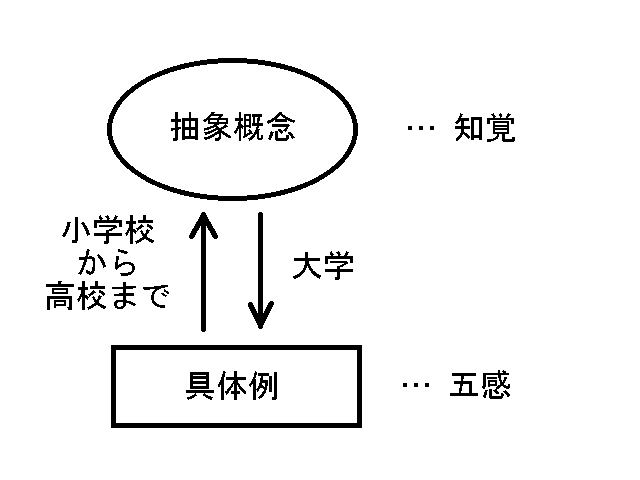
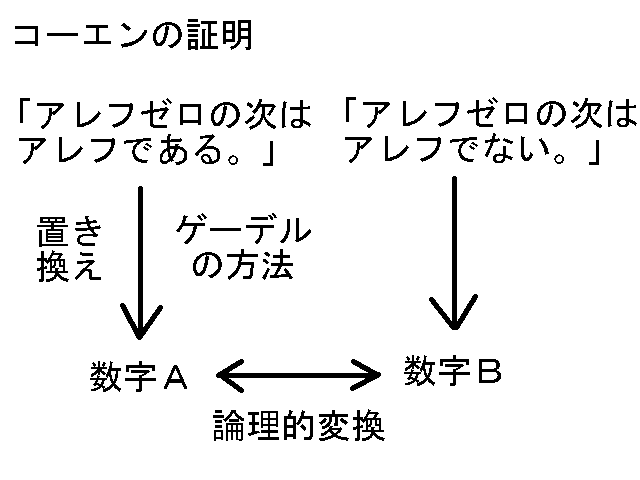
・知覚における抽象概念は、五感における具体的認識から作られる。だから、いくら記号をにらんで頭の中だけで考えても、記号の意味はわからない。自分がすでに知っていることから、その記号を意味づけないかぎり、その記号の意味はわからない。具体例から要らない意味を切り捨て抽象化することによって、記号の意味が見えてくる。五感における経験から不要な意味を取り除くことによって、洗練された知覚的概念が得られる。このプロセスがまず必要なのだ。 『現代解析学の祖ワイエルシュトラス』 ☆ h15.4.5 『定理と証明 』 ☆☆☆ h15.7.3 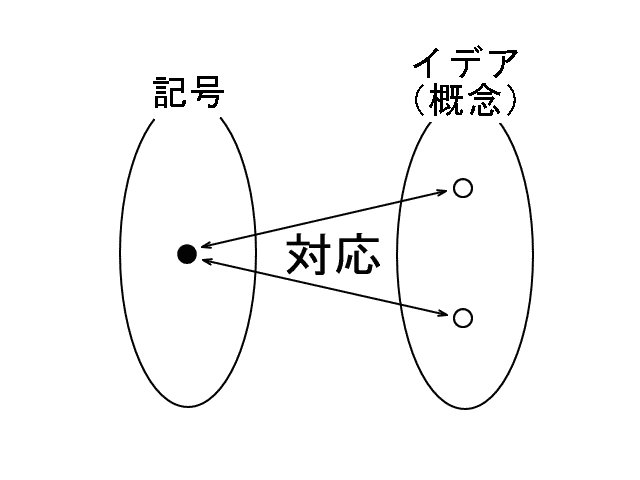 いわば、ユークリッドの第1〜第4公準までが記号(“点”とか“線”とか)を未知数とした多元連立方程式のようなものであり、その解(記号の中身としてのイデア=意味)が一意的でなかったために、第5公準の結果がそれぞれの解で違ってくるのである。 つづき(集合論における連続体仮説) 集合論にも公理系がある。つまり、集合はいくつかの公理によって定義されている。 公理系にはいくつかの言葉が用いられている。 ゲーデルが示したように、言葉の意味は自然数である。つまり、言葉(記号)と自然数の間に対応付けがある。[ユークリッド幾何学や非ユークリッド幾何学では、言葉の意味は図形(イメージ;視覚像)であり、ユークリッド幾何学と非ユークリッド幾何学とでは同じ言葉に対応する図形が違ったのである。煎じ詰めれば、一般的に言葉の意味は自然数だと言える。とりわけ抽象的な集合論では、言葉の意味は最も素朴な存在である自然数にしてしまうのがいい。〈ついでに、哲学について言えば、哲学とはつまるところ認識論すなわち‘認識とは何か?’であり、認識と言う言葉の意味の違いがさまざまの哲学体系を生み出すのだ。実在哲学においては、認識とは‘脳細胞の神経興奮によって感覚が発生する’ことである。ちなみに、その他の下賤哲学では認識とは‘見るものと見られるものが出会う’ことだそうだ。〉] ところが、この対応付けは一意的ではなかった!(ただし、連続体仮設を除いて) ここのところの事情が上の非ユークリッド幾何学と同じなのである。 そのために、連続体仮説が成り立つ場合と成り立たない場合の両方がありえるのである。 (コーエンの証明) 問題点 1.そもそも言葉の意味が定まらずに、どうやって研究ができるのか? 数学者はいったい毎日何をやっているのか!?数学者はふてぶてしいかぎりだ。 2.どうすれば言葉の意味が一意的に定まるのか? 連立方程式のように、単語数よりも文(文は単語と単語の関係式だから)の数のほうが多ければ、単語の意味が一意的に決まるのだろうか。 ゲーデルの方法では、言葉の意味を自然数で表す。つまり、すべての言葉の意味が自然数で表されるとゲーデルが規定したのだ。ところで、自然数は2進法で1と0の組合せとして表され、一方脳細胞の状態は興奮するかしないかの1か0かだから、結局言葉の意味を脳細胞の上に乗せたことになり、私の実在哲学の方法と一致している。 『4色問題』☆(アッペル&ハーケンの証明より) h16.3.23 国の数がある程度多くなると、(地図が4色で塗れるかどうかだけを問題とするときには)それより国数の小さい地図に全部“還元できる”。 だから、あとはコンピューターでシラミつぶしに4色で塗れるかどうか調べればよい。 『どうして分数の割り算では分母と分子が入れ替わるのか?』☆(宮崎アニメ「思ひでぽろぽろ」より) h16.10.13 まず、分数を整数で割る場合を考える。例えば、3/4÷2=3/4×1/2=3/8だが、2=2/1で1/2は2/1の分母と分子を入れ替えたもの(逆数)である。つまり、3/4÷2=3/4÷2/1=3/4×1/2(分母と分子を入れ替えて掛ける)=3/8となる。 これを一般化して、分数を分数で割る場合にも、『分母と分子を入れ替えて掛ける』と考える。こうすれば上手くいくので、これでいいのだ。(終) 『どうして負の数に負の数を掛けると正の数になるのか?』☆ h16.10.13 『マイマイでプラ』だから。(by鶴沢) まずは、理屈ぬきで憶えよう。 それで、矛盾が出なければOKだ。〔論理的拡張〕 『数学とは何か?』☆ h16.10.14 自分だけの数(一般には何らかの概念)を作って、それに関する命題を作ること。〔要するに、自分の得意な(特異な)センスを活かすことだ。そもそも‘得意’とは、自分の五感界における経験を思考によって分解して、知覚界に‘意味(概念、イデア)を得る’ことだ。概念が出来るか出来ないかは、努力と運にかかっている。〕 『…の意味』☆☆ h18.5.12 π=3.14159265…における…の意味は、「もし仮りに人間に小数第無限位までわかる能力があるとしたとき、見えてくる数字の列」を表している。“人間に小数第無限位までわかる能力がある”と考えないかぎり、人間が実数を扱うことはできない。つまり、実数は人間に“小数第無限位まで見る目”があってはじめて見えてくるものなのだ。 このように、数学では、人間に実際にはできないことをできると仮定して、その仮定の下でわかることを考えるのである。 『現代数学における微分の定義』 h18.5.26 人間に小数第∞位まで見える目があるとして、ω=0.00…1(小数第∞位が1)の数を考える。 ωは無限小である。 Nを有限の数として、Nωも無限小である。(つまり、無限小はひとつの数ではなく同値類である。) このとき、無限小量ωに対して、f(x+ω)-f(x)=f'(x)ωを満たすf'(x)をf(x)の導関数と定義する。[ただし、ここでの等号は高位の無限小を無視するものとする。] 『デデキントの切断』 h22.6.29 デデキントの切断の目的は、『集合論の概念で実数を定義する』ことである。 現代数学の精神は、集合論の上にその他の数学の体系を構築することである。 デデキントはそれを最初にやった人なのだ。 ペアノの自然数論も同じことである。つまり、ペアノは集合論の上に自然数の体系を築[きず]いたのだ。 ベルトランのパラドックス h22.10.12 『単位円(半径の長さ1がの円)周上に“でたらめ”に弦を引いた時、その弦の長さが円に内接する正三角形の辺(長さ√3)よりも長くなる確率を求めよ。』 私は“でたらめ”とは一様分布のことだと思う。 つまり、弦の長さとは点(1,0)から始めて円周に沿って左回りに0〜2πまで一様にランダムにふたつの点を取ったとき、その線分の長さを意味するのだと思う。 それならコンピューターシミュレーションで実験できるからやってみればいい。 答えは一意的に決まるはずである。[これだと、リンクの【考え方1】の1/3になると思う。] つまり、ベルトランのパラドックスは“でたらめ”の意味をはっきりさせよと言いたいのである。私はまず最初に“でたらめ”の意味をはっきりさせて考えたから問題がなかったのである。 非ユークリッド幾何学 h23.8.6 ユークリッド幾何学の公準は言葉だけで書かれていたので、ユークリッド幾何学の公準に用いられている言葉に幾何学図形が対応すると考えた。つまり、言葉の意味が幾何学図形だと考えたのである。 そこで、数学者はこれまでの言葉と幾何学図形の対応を変えることによって、ユークリッドの第1公準から第4公準までを満たし、第5公準を満たさないことができないだろうかと考えたのである。“たこ”には空に揚[あ]げる凧と海にいる蛸があるようなものである。 そうして出来たのが非ユークリッド幾何学である。 そうすることによって、第5公準が第1公準から第4公準によって導かれないことが証明されたのである。 微積分の基礎 h24.1.14 微積分は有理数の上ではできない。[有理数とは“1”と“四則演算”から有限回の演算で得られるすべての数である。] 微積分は実数の上でないとできない。 有理数の集合に無限大を加えた集合(厳密には体[たい])が実数である。1/無限大が無限小なので、実数の集合には“無限小”があるので、実数の上では微積分がやれるのである。 つまり、微積分をやるためには、まず無限小がなければならない。ところが、有理数の集合には無限小がない。だから、有理数の集合に無限大を加えた数の集合を考えて、1/無限大を無限小と考えて有理数の集合に無限小を加えた実数の集合を作らねばならないのである。 実数の集合には無限小や無限大があるから、自由に微積分がやれるのである。 つまり、x→1とは、“xが限りなく1に近づく”ということだが、“xが1から無限小だけ違う数である”ということでもある。つまり、“x=1+無限小、x=1+1/∞”ということである。 実際に、一辺の長さ1の正方形の対角線(つまり√2)や半径1の円の円周や円の面積(つまり2πやπ)などの量が実在するから、この世界は実数の世界なのである。だから、まず実数が出来なければ物理学がやれなかったのである。つまり、実数とは“実在する数”と言うことである。 つまり、x→1とは、“xが限りなく1に近づく”ということだが、“xが1から無限小だけ違う数である”ということでもある。つまり、x=1+1/∞ということである。例えば、x→1のとき(x2−1)/(x−1)の値は、普通の微積分では2だが、無限小のある世界では2+ε(無限小)になる。答えがちょっと違う。人間が測定するときにはε(無限小)は測れないので2+εが2になる。つまり、2+εは“測定する”と2になる。つまり、微積分の世界では、人間は無限小を加えたり除[の]けたりしている。宇宙は無限小のある世界だが、人間に測定できる世界は無限小のない世界なのである。人間はこの二つの世界の間を行ったり来たりしているのである。人間が“人間に測定できない量”(無限小のこと)を考えたから宇宙のことがわかったのである。微積分と同じように、量子力学では“人間に測定できない物質の状態”を考える。微積分は量子力学に似ている。つまり、眼で見えることにこだわると宇宙のことがわからない。眼で見えることにこだわらなくなってはじめて宇宙のことがわかるのである。 『不完全性定理』 h24.10.23 数学も科学と同じようなものである。 科学で実在の物を言葉で書いているように、 数学では架空の物を言葉で書いているのである。 ただ、科学と数学では違うところがある。 科学では言葉がまちがっていることがある。言葉が実在の物によって直されることがある。 しかし、数学では言葉がまちがっていることがない。言葉が架空の物によって直されることがない。 ただ、『不完全性定理』が教えるように、言葉では書けないことがつねにあるのである。 ユークリッド幾何学と連立方程式 h24.11.3 ユークリッド幾何学の第1〜4公準を連立方程式と見なす。“点”とか“直線”とか“交わる”とかを連立方程式の未知数と見なす。 ユークリッド幾何学の公準では、未知数の数のほうが方程式の数よりも多いから、解が一意的に定まらない。 だから、ユークリッドの解以外にも解がある。 それが、非ユークリッド幾何学である。 だから、第5公準の否定も成り立つのである。 公理主義 h24.11.8 言葉の中身は自分で自由に考えて作ればいい。 言葉の中身はめいめい違っていてもかまわない。 公理系を満足しさえすれば何でもいい。 言葉はみんなで共通だが、言葉の中身は各自の自由だ。 5次方程式が冪根[べきこん]で解けない証明 h27.6.13 集合の『自己同型写像』を考える。自己同型写像とは、集合から集合自身への和と積の両方を保つ写像のことである。(詳[くわ]しくは数学の本を見てね。) 有理数の集合に冪根を付け足して行った集合の自己同型写像は巡回群の積になる。C=C1×C2×…×Cn。一方、有理数の集合に五次方程式の解を付け足した集合の自己同型写像は5次の対称群になる。ところが、5次の対称群は巡回群の積にはならない。だから、5次方程式は冪根では解けないのである。証明終わり。(「有理数の集合に冪根を添加して行った集合」に「有理数の集合に方程式の解を付け足した集合」が含まれなければ方程式が代数的に解けないことになるから、巡回群の積の部分群に対称群がないことを証明すればいい。) ガロアは世界で一番最初に『自己同型写像』を考え出した人である。だから、偉大なのである。 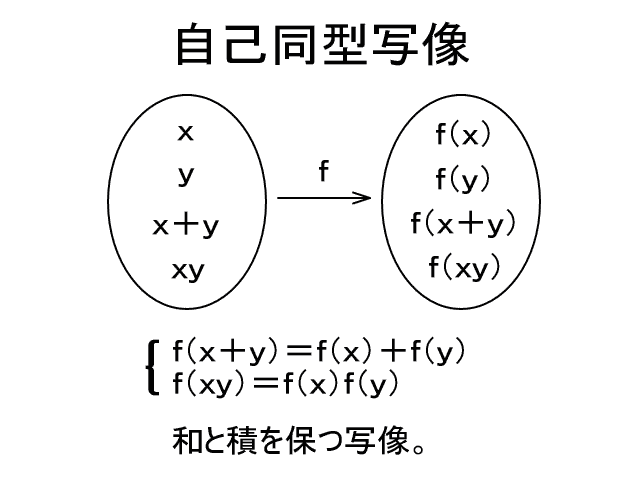 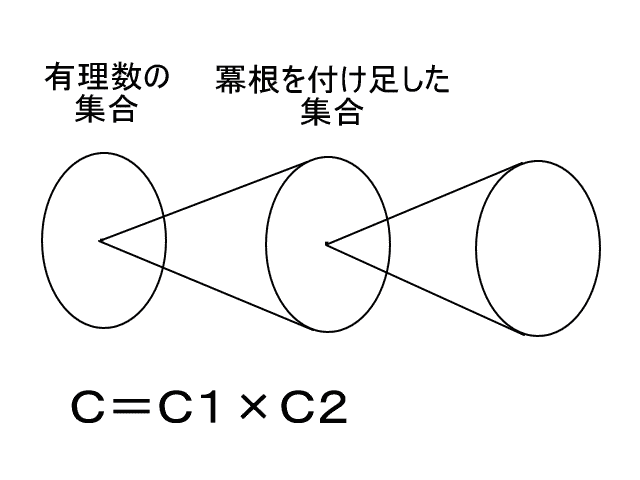 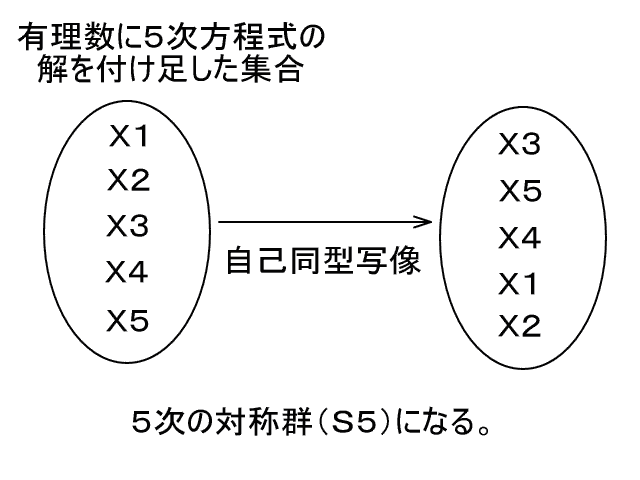 群論をどのように勉強すればいいか? h27.6.16 群論は数学科の2回生から講義が始まる。数学科の学生にとっては群論を理解できるかできないかで人生がハッピーかどうかが決まる。群論を理解できるかどうかがネックである。関所である。微積分学や複素解析学はまだなんとかなるが、群論は抽象的すぎてとっつきにくくてもはやお手上げである。集合論は簡単だが、それにひとつ演算が加わって群論になるといきなり難しくなる。 群とは演算で閉じた集合であり、群論とは演算で閉じた集合についてその性質を調べることである。整数論が整数の性質について調べるのと同じことである。 群とは例えば18のように整数のようなものであり、部分群とは例えば18に対する12のようにある整数以下の(正の)整数のようなものであり、正規部分群は例えば18に対する6のように整数の約数のようなものであり、単純群とは例えば3のように整数の素数のようなものである。群を正規部分群で割るとこれまた群になる。例えば18を6で割った商の3がこれまた整数になるのと同じことである。剰余類(整数をある数で割った余り)がこれまた整数のようになるのと同じことである。群は整数や剰余類を抽象化したものである。群論はガウスの整数論の剰余類を深めたものである。だから、整数や剰余類についての知識を頭に置きながら群を理解すれば、理解が容易になる。剰余類群(剰余類から成る集合)を例にしながら群論を考えれば理解しやすくなる。シロウトがいきなり群論を理解するのは難しい。だから、群論を学ぶ前に、もっと具体的でわかりやすい剰余類群などについてよく勉強すればいい。何か一つ具体的なことについてよく知ってから、もっと抽象的なことを勉強すればいい。 群論は言葉が難しいだけで、中身は整数論や剰余類論とあまり変わらない。見かけの難しさに騙[だま]されて頭を不必要に混乱させてはいけない。最近の抽象数学は見かけが難しいだけで中身は簡単である。馬鹿がわざとに難しい言葉を使って数学の基礎は整数にある。だから、整数についてまずよく勉強することが大事なのである。言葉の意味は眼で見えないからわかりにくい。眼で見てわかるようにすればわかりやすい。整数や剰余類や置換などは眼で見えるからわかりやすい。群論では例えば置換群を具体例にとって定理の意味を考えながら勉強して行けばいい。(そこまで勉強する意欲があればの話だが…。そんなことを勉強する暇があったら、もっと実在に目を向けて実在のことについて考えて実在のことを知ったほうがいい。数学によっぽど興味がある人、数学がよっぽど得意な人、数学で食べている人以外は数学について考えないほうがいい。群論が理解できなかったら、数学科をやめてほかの学科に変わったほうがいいかもしれない(笑)。) 正規部分群 h27.11.16 一般に、群の元は非可換である(ab≠ba)。 しかし、元が群れになって群になると可換になる(HN=NH)。それが正規部分群である。 非可換なものが集まると可換になる。 そこが群の面白さである。 どうしてラマヌジャンは数学が得意だったのか? h27.12.18 優れた音楽家は自分の得意な“作曲パターン”を普通の人よりもたくさん持っている。音楽家は自分の得意な作曲パターンを駆使[くし]していろんな曲を作る。 それと同じように、ラマヌジャンは自分の得意な“数学の思考パターン”(つまり数学の世界における考え方)を普通の人間よりもはるかにたくさん持っていたのだ。 ラマヌジャンは小さい子供のころに1から1万までの自然数について考える中で“数学において用いられる思考パターン”を身に付けていったのである。大人になってそれらを駆使していろんな数式を書いたのである。音楽を作るのも数式を作るのも同じことだ。 私もこれまでの人生で数学や物理学を勉強する中で“学問の思考パターン”をいくつか身に付けていった。それらを駆使して、政府について考えて、約10年かけてようやく『政府が民主主義の芝居をする権力団体(国民みんなを虐[いじ]めて国を平和にする団体)である』ことがわかったのである(私の哲学日記を参照)。 学問の世界では分野を超えて“思考パターン”を利用できる。だから、小さい子供のころからいろんなことを勉強していろんな“思考パターン”を身に付けて持っていることが大事なのである。 例えば、私の哲学日記[22365]で政府の民主主義の芝居を“架空の世界”の中に入れて“現実の世界”との対立で理解したことは画期的だが、それはテレビで見たアニメやマンガの影響である。 テレビのアニメやマンガは“なんでもあり”である。アニメやマンガは架空の世界なので作者が自分の都合のいいように設定を決められる。それと同じように、政府の民主主義の芝居も架空の世界である。架空の世界では“なんでもあり”なので、政府は自分の都合のいいように物事を決めている。政府は間接民主制で自分が国民みんなに従っていて国民みんなの役に立つことをやっていて自分に国家権力があって国民みんなが自分に従わねばならない“ことにしている”のである。政府は多数決で法律や政策を決めることができて国民みんなに守らせることができる“ことにしている”のである。しかし、現実の世界では間接民主制では政府は国民みんなに従ったことにならないから政府に国家権力はなく国民は政府に従う必要はない。現実の世界では多数決の原理はないから政府は多数決で法律や政策を決めて国民みんなに守らせることはできない。国民の多くは政府の芝居に呑[の]まれて芝居の世界に入り込んでいるために、政府に従って政府が決めた法律や政策を守っているのである。(『宇宙刑事シャリバン』(1983〜84)“幻夢界に引きずり込め”)例えば、選挙の投票は国民が政府の芝居の世界に自分から入り込むことである。現実の世界では国民は政府に従わなくてもよく、政府が決めた法律や政策を守らなくていい。国民は政府の民主主義の芝居の世界から抜け出して現実の世界に戻れば、政府に従わなくてもよくなって自由の身になるのである。 テレビで見たアニメやマンガでさえも学問においては役に立つことがある。自分の人生のすべてを活かして問題と戦わなければならないのである。 5次方程式はどうして代数的に解けないか?(ガロアの証明) h28.8.22 代数方程式の解の“同型写像”は解の置換群(対称群)である。基礎体(つまり有理数体)上で独立した超越数を考えれば、対称群になるのは明らかである。 一方、冪根[べきこん]を付け足して数を拡張したときの同型写像は巡回群の積になる。 ガロアが発見した定理によれば、『解の置換群の部分群と拡大体の中間体との間には必ず一対一の対応がつく』から(詳[くわ]しいことは本を読んでね)、解の置換群の部分群についてだけ考えればいい。例えば、3次方程式の解の置換群はS3=C2×C3だから、必ず3次の冪根を付け足した中間体を経ないといけないことがわかるから3次の冪根には必ず虚数が含まれるから、3次方程式の解の公式には必ず虚数が含まれることがわかる。 1次2次3次4次の対称群までは巡回群の積になる。しかし、5次の対称群はどうしても巡回群の積にならない。だから、5次方程式は代数的に解けない(証明終わり)。 1+1≠2? h30.1.11 非ユークリッド幾何学のように「1+1≠2」なのに“矛盾のない数の体系”が作れないかなあ? 平行線の定理(第5公準)が成り立たないのに第1〜第4公準が成り立つ幾何学の体系が作れるように、「1+1≠2」なのにほかの(自然または実)数の原理(つまり公理)が成り立つような数の体系が作れるかもしれない。 それは非ペアノ自然数とか非デデキント実数と呼ばれるかもしれない。 デデキントの実数モデルの直線を非ユークリッド幾何学の空間で曲げてやれば出来るかもしれない。 |