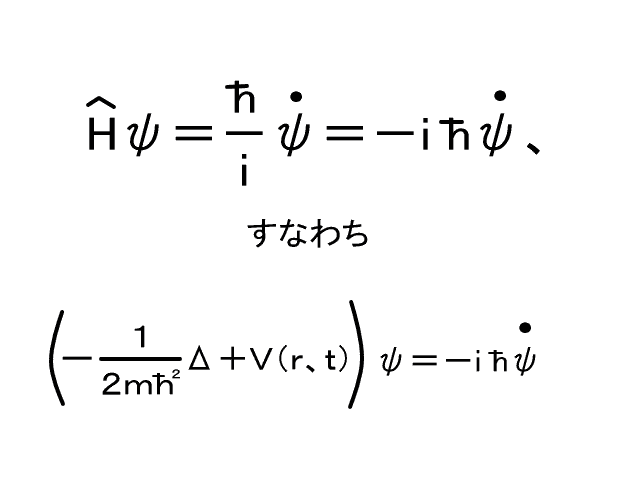|
わかる量子力学
1.あらすじ 2.観測問題 3.瞬間移動
4.シュレーディンガーの猫 5.光子の位置
6.量子力学メモ
1.あらすじ(h13.10.27)
自分が実在哲学を名乗る以上、いくら日本人にとっての実在が哲学認識であるとはいえ、物理学としての実在についても考えないでは済まされない。それが実在哲学第一人者としての私の使命だ。
大学時代、量子力学の本をいろいろ買って読んでみたけど、基礎がわかるものはひとつもなかった。いくら数式で書かれていても、基になる論理の枠組みがわかっていなければ、ただの無意味な記号の計算にすぎない。これでは数学がわかっただけで、物理学がわかったとはいえない。
量子力学の難しさは、その数学的な計算の難しさにもあるが、量子力学に出てくる概念の理解の難しさにもあるのだ。
それでは、いよいよ私の量子力学の講義を始めよう。
量子力学の創始者はマックス=プランクというおじいさんだ。彼は「光のエネルギーが飛び飛びの値しかとらない」ことを仮定して黒体輻射の問題を解いたが、彼自身この仮定を『自分がニュートン以来の大発見をした』と言って喜んだように、古典力学の世界の内にはない新しい原理であることを見抜いていた。おじいさんの割にはずいぶん大胆なことをしたもんだ。しかし、彼は量子力学の世界の一端を垣間見ただけで、彼一人の手で無矛盾な世界を作り上げるまでには到底至らなかった。とにかく、このおじいさんが人類史上はじめて量子力学の世界に足を踏み入れた。この人だけが、やたらおじいさんで、後の人がみな若手なのは不思議なことだ。
当時問題だったのは、原子の構造である。古典力学の理論では、どうしても原子が安定に存在し得ない。そろそろニュートン力学の限界が見え始めた。どうやらものすごく小さな物体についてはニュートン力学が適用できなくなるらしい。大きい物体に見慣れすぎたわれわれの目がだまされていたらしい。ニールス=ボーアというイギリス人が出てきて、「角運動量が飛び飛びである」と仮定して、あっさりこの問題を解決してしまった。
イギリス人は眼で見えるように問題を解くのが得意だが、フランス人のやり方はもっと抽象的で大胆だ。
ド・ブロイというフランス人は、アインシュタインの「光はツブツブである」という仮定を受けて、その逆に、「電子は波である」とした。すべての物質に粒子=波の二重性があるとしたのである。ここまで一般化されると、かなり原理っぽくなって、量子力学に近づいてきたなあという感じがする。
最後にとどめを刺したのは、エルビン=シュレーディンガーといういつもパイプをくわえている変なドイツ人だ。彼は、ドブロイの物質波の概念を真に受けて、物質波の運動方程式を立てた。運動方程式の解を波動関数と名づけた。シュレーディンガーにとっての波動関数の意味は、まさしく古典力学における波そのものであって、彼にとっての素粒子像とは、“粒子の波乗り”にほかならなかったのである。(ド・ブロイだったかもしれない。間違っていたらすいません。)ノーベル賞を取った彼ですら、まだ古典力学の世界を抜け切れなかったのだ。
ここで大抵の教科書は書くのをやめてしまっているので、うやむやなままで終わってしまうことになるのだ。2年間の講義が全部パーになってしまうのだ。
シュレディンガーですら、波動関数Ψに余計な意味があった。古典力学における素粒子像は点(r、p)であり、シュレーディンガーにおけるそれは粒子の波乗りであった。じつはそもそもΨに余計な意味づけはいらないのだ。《Ψ自体を素粒子の実体と見なせばいい》のだ。この宇宙は複素数のある4次元空間なのだ。そこで私はこのΨを“実体関数”と命名する。《Ψが実体だ。あとは測定値にすぎない。》あえて言えば、素粒子の姿は、アメーバが仮足を出して動いているのに似ている。
もともとΨのほうが素粒子の実体なのであるから、電子線のヤングの実験なんかでは、むしろ観測された電子が一個の点であることのほうが不思議なくらいだ。観測界においてはひとつの値しか観測されないことこそが謎だ。(これを観測問題と呼ぶ。)
量子力学の歴史
プランクの量子仮説…エネルギーの量子化=古典力学(ニュートン力学)の世界の内にない原理
↓とりこみ
ボーア模型…角運動量の量子化
↓とりこみ
ド・ブロイの物質波
↓とりこみ
シュレーディンガーの波動方程式…Ψは波動関数
↓とりこみ
私の実体関数Ψ…Ψそのものが素粒子の実体だ。観測値はΨに従属する。


それにつけてもなお、量子力学には上で述べた観測の問題など、よくわからないところがある。実体界と観測界の二本立ての世界観は、じつのところ腑に落ちない。実体と観測を統一する理論が今のところない。そこは現在の量子力学の欠点である。現在の量子力学は完全ではないが、しかし良い所が多い理論であることに違いはない。量子力学は今なお発展途上の理論である。量子力学の良い所だけをよく見て、悪いところは当分の間無視することにしようではないか。
2.観測問題を考える。(h13.11.3)

物理量Aを測定する前は、量子Ψは波動方程式ih∂Ψ/∂t=HΨ(ただしhはhバーのこと)に従っている。
物理量Aを測定しようとすると、量子Ψには測定に伴う‘力’Aが働き、ΨからAの固有関数のひとつφ1へ変化してしまう。つまり、測定の前後でハミルトニアンHが変化してH=H(測定前)→H(途中)→A=H(測定後)となり、そのシュレーディンガー方程式を解くと、Ψ→φ1に一意的に変化が決定される。
Aの固有関数はたくさんあるが、多数の原子からなる測定装置の微妙な状態の違いによって、測定途中のハミルトニアンH(途中)もそれぞれ違うので、どこのAの固有関数に収束(変化)するかまで細かいことはわからない。要するに、統計力学における確率の扱いと同じなのだ。観測系には多くの原子(量子)が含まれているために、測定値が確率的にしかわからないのだ。つまり、量子ΨはS式(シュレーディンガー方程式のこと)に従いながら連続的に固有関数φ1に変化するのであって、ボルンの原理の言うように測った瞬間に不連続的に変わるのではない。こう考えれば、量子力学には一時しのぎのボルンの原理がなくてもS方程式だけあれば十分であり、量子力学における確率も統計力学と同じように見かけの確率として考えればよく、観測界が実体界に吸収され、両者が統一されたことになる。
…以上は私が6年ほど前学生だったころに考えたことであり、今でもこの考えは少しも変わっていない。
しかし、こうなると問題になるのがEPRパラドックスだ。EPRパラドックスとは、2個の粒子のスピンが超光速で瞬間的に相関し合うというものである。超光速ってところが、相対論に引っかかるのだ。
でも、この変化はシュレーディンガー方程式に従う(後述の*参照)から、量子力学的にはOKだ。そもそも量子原理は相対論の世界の外にあるから、むしろこの非局所的相関を相対論の世界の内に取り込んで、相対論の世界のほうを拡張しなければならない。
質量0のもの(例えば情報)なら光速を超えても大丈夫だろう。1ビットの情報子が超光速で伝播したと考えればよい。

相対論の世界の外にある問題を相対論の内から見て批判してはならない。かつての古典力学と相対論の関係と同じだ。

相対論がタイムマシンが存在しないといっても、量子力学の世界ではもはやそれは常識としては通用しない。相対論の世界の外にある量子力学の世界ではタイムマシンが作れるかもしれないのだ。
タイムマシンで自分が未来から現在に帰ってきたら、現在の自分が二人いることになるが、これって量子力学の物質波Ψと似ているとは思わないか?!
*)S方程式(を解くこと)から、非局所的相関が出てくる。
Ψ=ψA↑ψB↓+ψA↓ψB↑
ψAが粒子Aの測定によってψA↑に収束するのはS式による局所的連続的変化であるが、ψBが粒子Aの測定によってψB↓に収束するのは非局所的連続的変化である。いわば、量子力学の世界には2種類の変化(運動)があるのだ。
古典力学や相対論に世界にはシュレーディンガーの猫はもちろんいなかったが、量子力学の世界の内にはSの猫(生きている猫と死んでいる猫の中間の猫)が住んでいる。もはや状態変化のスピードなどは、まったく問題にならないのだ。
こんな量子力学の世界が、現在考えられているなかで最も実在に近い世界観である。
むかしI波書店とS華房の本を買って読んだことがある。上のようなことは一応書くには書いてあるけど、著者の気持ちの入り方が弱くて、読んでも何が言いたいのかわからなかった。
3.瞬間移動(平成13年11月11日)
Ψ(t=0)=δとする。少し時間がたった後のΨは、シュレーディンガー方程式により、

のようになる。
このΨの広がりは質量m→0で大きくなるから、位置の測定によって光速cを超える移動が可能になる。シュレーディンガー方程式自体は、非相対論的だが、本質的には問題ない。しかし、mが大きいときには広がりが0に近づき、遠方の確率も厳密には0ではないが、極めて小さいために実際にはそこに現れることはない。統計力学において体系が急に爆発したり、温度が1兆度になったりすることがないように、量子力学においても確率が小さいところでは、実際にはその状態が出現することはないと見なしてよい。
量子力学の世界は相対論の世界の外にあるから、物質波の収縮の速さは問題にならない。Ψが超光速で収縮してもかまわない。したがって、ボルンの原理は不要であり、物質はシュレーディンガー方程式だけに従うと考えてよい。
物質波の広がりをひとつの粒子内での相関と考えれば、EPRパラドックスの例のように、Ψが超光速で変化することは現にあり得ることなのである。
4.シュレーディンガーの猫(平成13年11月11日)
シュレディンガーの猫は物質波の拡大顕微鏡のようなものだ。しかし、物質波は収縮する。物質波がどこで収縮するかが問題だ。答えはガイガーカウンターだ。なぜなら、ガイガーカウンターは‘多原子から成る’物体で、放射性元素が崩壊したか否かが‘測れる’からである。だから、猫の生死がわからないのは、ツボの中のサイコロと同じ見かけの確率であって、箱の中では生きた猫か死んだ猫かのどっちかが入っているのである。
工夫をすれば、箱の中でいわゆるシュレディンガーの猫(生きた猫と死んだ猫の中間の猫)が実現できるかもしれない。その猫は人が見たことによってシュレーディンガーの方程式に従いながら連続的に生きた猫か死んだ猫かのどちらかに収縮するのだ。Ψ中間がΨ生になるかΨ死になるかは、人の眼の微視的状態の違いによって決まる。(パチンコと同じ。)


Ψの変化はいつでもシュレーディンガー方程式に従う。Ψについて、ある物理量Aを測定するとき、Ψはミクロにはシュレーディンガー方程式に従って変化するものの、それを具体的に解いて収縮先を求めることは難しいので、その代わりに統計力学と同じように考えて、マクロに見たときΨの収縮先は物理量Aの固有関数φのどれかになり、その確率は|〈φ|Ψ〉|^2で与えられるとするのである。ボルンの原理は、シュレーディンガー方程式に基づいて証明すべき定理のひとつなのである。
5.光子の位置(平成13年11月11日)
空間的に一様な光子をフィルムにぶつけて光子の位置を測定する実験について考える。

このときフィルム上の電子の濃い所に光子の物質波が集まってくる。
フィルム上の電子密度が完全に一様であれば、光子の物質波は収束せず、フィルムには何も写らない。しかし、実際にはフィルム上の一点に光子の物質波が収縮する。これは、現実にあるフィルムには多かれ少なかれ電子密度の濃淡が存在するからである。
光子の位置測定の実験は、実際には一様な光子を用いてフィルム上の電子密度の一番濃いところを測定しているようなものだ。測るものが逆に測られているワケだ。
一般に、Ψの物理量Aを測定するとき、同じΨであれば、逆に測定装置のほうがΨによって測られることになる。同じΨでも収縮先(物理量)が違ってくるのは、ミクロに見た観測装置の状態がそれぞれ測定ごとに違っているからである。
6.量子力学メモ
『観測問題』 h13.12.15
観測問題とは、シュレーディンガー方程式に基づいてボルンの原理を証明することである。
量子力学の世界が実在の宇宙に最も近く、量子力学の世界とはシュレーディンガー方程式に従う世界にほかならず、観測はこの宇宙におけるひとつの自然現象であるから、観測もシュレーディンガー方程式によって説明されるはずである。
『Ψ』 h14.5.20
素粒子像は点ではなくて雲である。古典力学で物体を点と見なすことに慣れすぎているから、量子力学がわかりにくいのだ。
人間の頭の中では‘点’が一番イメージしやすい単純な形だけれども、宇宙は人間の頭の都合で出来てはいない。素粒子が雲だと言ったら雲なのだ。素粒子は一個の(ひとかたまりの)雲なのだ。もとから雲であるものに、いくら点のイメージを当てはめても合うはずがない。
Ψの雲そのものが素粒子の真の姿であり、宇宙にとっては(ちょうど人間の頭にとっての点のように)最も基本的な存在形態であって、‘雲’の意味についてこれ以上解説することが出来ない。
|Ψ(物理量)|^2によって、Ψと観測された物理量との関係をつけることができる。このことは本来シュレーディンガー方程式によって証明すべき事柄だけれども、今のところその証明は未完成だから、『ボルンの原理』と言ってすませる。
『ボルンの原理に対する考え方』 h14.9.21
宇宙の万物は完全にシュレーディンガー方程式に従う。
ただし、観測系が絡んでくると方程式が複雑すぎて解けないので、
シュレーディンガー方程式を解く代わりにボルンの原理を用いる。
『イメージとイデア(現代物理のこころ)』 h14.9.25
P.A.M.Diracは物質の実体はイメージ(視覚像)ではもはやわからず、イデア(知覚的代数的概念)でなければ理解できないものだとした。
Einsteinは物質のイメージ(視覚像)にこだわりつづけたので、量子力学(物質の真実)がわからなかった。
物質の実体は五感ではなく知覚でなければ理解できない。
五感にこだわってはならない。(Einsteinが五感=現象にこだわるところにGoethe以来のドイツ気質が表れている。)
現代物理における‘わかる’とは、‘五感(とくに眼)で見える’ことではなく‘知覚で見える’ことである。
物理学の歴史は、哲学の歴史でもある。
量子力学を勉強するときには、イメージ(視覚像)でわかろうとせずに、イデア(代数的概念、ことば)だけでわかるようなつもりで勉強するといい。
なぜなら、実在は五感(絵)ではなく知覚(ことば)によってとらえられるからである。
古典力学はイメージの力学だが、解析力学はイデアの力学である。
量子力学が‘眼に見えない’のは解析力学をもとにしているのでやむをえない。
人間はどこまで五感のウソ(例えば、近接作用)を見破れるか?!
『観測問題とシュレーディンガーの猫』 h14.9.29
『この宇宙にあるすべての物質は厳密にシュレーディンガー方程式に従う(だから、確率は要らない)のであり、多くの素粒子から成る観測系が絡むと方程式が複雑で解けなくなるから便宜的にボルンの原理を使う。』とすれば、要するに「多くの粒子が絡んでくると波動関数の収縮が起こる。」ことになる。したがって、シュレーディンガーの猫の場合には、「波動関数の収縮は多くの原子から成るガイガーカウンターのところで起こるから、箱の中の猫は生きているか死んでいるかのどちらか一方の状態しかとらない」ことになる。「生きている猫と死んでいる猫の重ね合わせた状態の猫」なんて実在しないのだ。
それとも『‘感覚子’が発生すると波動関数が収縮する。』のだろうか。そうだとしても、猫には脳があり猫が認識すると感覚子が発生するから、やはり箱の中の猫は生きているか死んでいるかのどちらか一方の状態しかとらないことになる。
『超光速通信の原理』 h14.10.15
EPRパラドックスの実験事実を使う。
今、地球と火星の中間にある小惑星から、互いに反対のスピンを持った光子を発射する。地球において光子のスピンの向きを測定することを1、しないことを0としてこれらを信号とすれば、火星において超光速で(と言うか瞬間的に同時に)信号を送ることができる。
この原理を情報処理に応用すれば、
処理速度∞のコンピューターが作れる。

平成15年4月22日
・波動関数とは、粒子と波の間をつなぐもの。素粒子は任意の形をとりうる。
・位置は素粒子の属性である。たとえば、スイスの高原に別荘を持っている金持ちに、「あなたのお家はどこですか?」とたずねると、「私のお家は日本とスイスなのよ。」と答える。つまり、このお金持ちの居場所は日本とスイスの2ヶ所ある。このように素粒子の居場所は同時に複数あっていい。
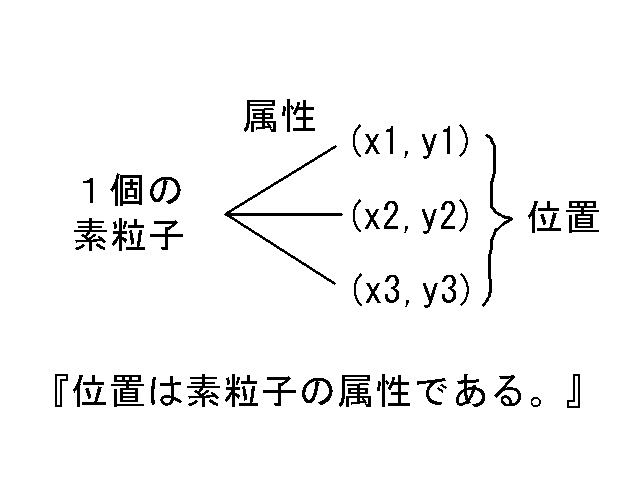
質量や電荷が素粒子の“属性”であるように、位置もまた素粒子の“属性”のひとつなのである。
・人間の肉眼で見える世界はせいぜいmmオーダーである。一方、量子力学の世界はnmオーダーである。肉眼の世界では素粒子の波としての広がりは無視されて点のように見えるが、量子力学の世界では素粒子の波としての広がりが利いてくる。肉眼の世界と量子の世界とでは全然見え方が違う。たとえば、大人と子供では身長が2倍も違わないが、子供のとき遊んだ遊園地を大人になって訪れてみると、ものすごくちっぽけに見えてまったく別世界のように見える。
平成15年5月2日
・位置は素粒子の属性である。(つづき)
つまり、『位置は物理量の一種』ということだ。ちょうど、運動量が物理量の一種であるように。
量子力学では一般に物理量は多価(同時に複数の値を取る)なので、位置も多価になる。その結果、素粒子の形態は雲になる。このように、素粒子の形態が雲なのは、‘素粒子が確率分布をする’(←高校までに習った古臭い確率概念で、素粒子という新しいものを無理に表そうとしたわかりづらい表現)からではなくて、『素粒子の位置が多価』だからである。つまり、位置が多価な一個の素粒子があるのだ。
『泡』 h15.5.6
実在の世界がどうなっているのか考えること、それが科学だ。
それは、さて置き、
『ゆく川の水は絶えずして、よどみに浮かぶうたかた(特異点=素粒子)はかつ消えかつ結びて、久しく留まりたるためしなし。世は‘定めなき’こそいみじけれ。(それは困る。運動方程式はどうした?)』川は水の流れである。水が流れると渦ができる。渦は水の流れの特異点である。同じように、素粒子は超時空間の特異点である。特異点の大きさは非常に小さいけれども、不確定性原理により有限の大きさがある。一方、EPR効果により光子は距離ゼロで相関しあう。光子は超時空間に開いた穴である。その小さな穴同士を結ぶ距離ゼロのトンネルを‘光子のスピンの向きを測定しました’という情報を荷う粒子が通って影響しあう。超時空間の特異点の穴は非常に小さいので、普通の物体は通れないが、小さい素粒子なら通過できる。すると4次元時空間の中を通るよりも近道(ほとんど距離ゼロ)ができる。もしも、その穴を広げることができたら、ドラえもんの‘どこでもドア’が作れる。(私が発狂寸前に見えた‘黒い穴’は、感覚子の通る特異点が広がったものだったかもしれない。)自動車が通るトンネル(超時空間の特異点)だって、小型車(極小の素粒子)ならそれを通って近道(いわゆるワープ)できるが、大型車(肉眼に見える大きさの物体)なら高さ制限で通れずに回り道(4次元時空間における通常の距離)をするしかない。つまり、2点間の距離は量子力学においては多価なのだ。[このあと図がありましたが、なくなってしまいました。(h17.6.18記)]
『観測問題』 h15.6.30
観測問題は、認識が絡んでくるので、物理学と哲学の両方が関与する複雑な問題である。
ところで、人が夢を見ているときは感覚が生じるが、何かを‘測定している’わけではない。
感覚は脳細胞の神経興奮に伴う自然現象にほかならない。
測定と感覚の発生とは無関係である。
測定のためには測定装置だけあればよく、人間はいらない。
実際、『量子力学入門』(並木美喜雄著;岩波新書)で見たように、位置を測定する装置を構成する原子数が増えると、それだけで観測される素粒子の位置の広がりが収束する。この間、人間はまったく関与しない。
『波粒(なみつぶ)』 h15.8.13
アインシュタインやド=ブロイらの研究により、光子や電子のような素粒子には粒(つぶ)と波(なみ)の両方の性質すなわち2重性があることがわかった。
一般に、すべての素粒子には2重性がある。
素粒子に2重性すなわち粒と波の両方の性質があるのは、素粒子が粒と波の中間状態にあるからである。
その中間状態を数学的に表したものが波動関数である。
素粒子は点(Δ)から波(exp(iθ))までのあらゆる形をとり、形は時間によって変化し、その形は素粒子に働く力によって決まる。
波動関数は最近(100年前)できた概念なので、波動関数に当てはまる日本語はまだない。
あえて言えば、波粒(なみつぶ)…か。
素粒子の世界では波動関数(Ψ)によって粒(Δ)と波(exp(iθ))は統合されているが、肉眼で見える世界では粒と波に別れている。
量子力学では概念に相当する日本語がまだ存在しない場合が多いので、“数学をもとにして”日本語を見ないと意味がわからなくなる。既知の日本語の単語の組合わせで数式の意味を無理に解釈するのではなく、逆に数式で量子力学の中に登場する日本語を意味付けしないといけない。
黙って数式を見て、あんまり日本語をしゃべるな!
波粒は粒でも波でもない新しい存在様態だから、
その物理的性質にはまだまだ未知のところが多い。
例えば、脳細胞の複雑な分子構造が感覚場を発生しても不思議ではない。
『トンネルダイオード』 h15.8.14
金属原子に不純物を加えることによって、原子間距離を自由にコントロールできる。
非対称性構造を持った金属に電場をかけたとき、電場の強さや向きによって原子間距離が微妙に変わる。
トンネル効果で、トンネルの長さが自由電子の波長の整数倍になったとき電子はトンネルを透過しやすくなる。
トンネルは金属原子の原子殻だと考えられる。
不純物を添加して非対称性を持たせた金属に電場をかけたとき電場の強さや向きによって原子殻間距離が変化し、電子の透過性すなわち電気伝導性が変化することがある。
これがトンネルダイオードの原理である。
現在の量子力学の問題点 h15.9.6
観測によって、観測される対象だけでなく、観測装置自体の(微視的)状態も変わるはずなのに、それが一切考慮されていない。観測される対象が観測によって変わるのなら、観測装置も対象からの反作用を受けて変わるはずである。それなのに、観測装置についての運動方程式がなく、観測によって観測装置が不変であると仮定されている。そのため、数学的には、観測装置だけから固有基底と固有値が決まる形をしている。いわば、対象と観測装置が足し算で捉えられ、掛け算になっていない。対象だけが考慮され、観測装置は(その具体的微視的構造が無視され)理想化して捉えられている。それでは、観測されるほう(微視的対象)だけがわかっていて観測するほう(測定装置)がわからないから、半分だけしかわからず、確率的にしか結果がわからないのも無理はない。観測されるほうとするほうの両方がわからなければ何もわからず、反対に観測されるほうとするほうの両方がわかれば確定的に(一意的に)結果がわかるはずである。
電子の形 h15.12.3
電子は古来より点、環、球体などと考えられてきた。
量子力学では、点はδ波という波の一種(一点に凝縮した波)だと考えられる。
いまや電子は周りの状況に応じていろんな形をとる波(というか体タイ、立体)だ。
例えば、水素分子において電子はピーナッツ形をしている。

超伝導 h16.1.28
固体中では電子が相互に力を及ぼし合って互いの形を決めている。
周囲からまったく力を受けないときの電子の形は、全空間に一様に広がった波だ。
周囲から力を受けることによって、波に濃淡のムラができる。
ところで、超伝導体中では電子波と電子波とが相互に作用し合っていて抵抗値が0になっていると考えられているが、実際には電子が完全な平面波ではないことから抵抗値が厳密には0でないはずである。
α線の散乱実験(ラザフォード) h16.1.31
ミクロの世界の現象はS式(シュレディンガー方程式の略)によって表され、ミクロとマクロの相互作用はボルンの原理によって表される。実際、α線の散乱実験では、α粒子(He原子核)と金の原子核はともにミクロだからS式によって表され、α粒子とフィルムの反応はミクロとマクロの反応だからボルンの原理に従う。
問題はミクロとマクロの境界でどうなるかだ。その世界においてはS式とボルンの原理が両方成り立つので、S式とボルンの原理とは本質的に同じことを表すはずである。
SとB(シュレーディンガー方程式とボルンの原理) h16.2.2
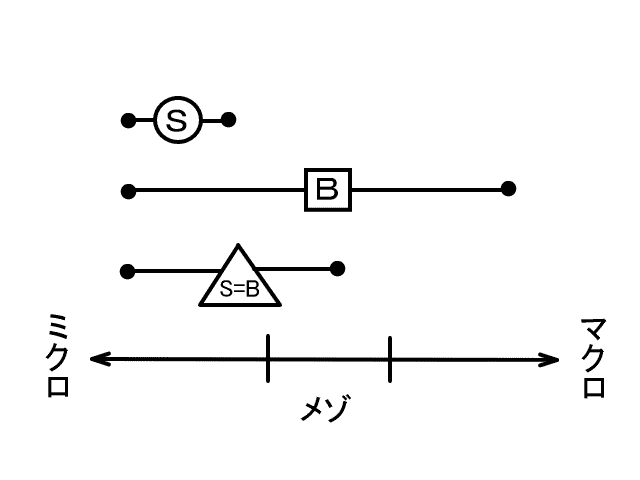
ミクロとミクロの反応はSに従う。
ミクロとマクロの反応はBに従う。
ミクロとメゾの反応はSにもBにも従う。つまり、SとBとは本質的には同じことの言い換えである。つまり、ミクロとマクロの反応も基本的にはSに従うが、実際にはSが解けないので、Sを解く代わりにBを用いる。
Sの解が一意的であるのにBで確率が登場するのは、マクロ系(観測装置)を構成する素粒子数が膨大であるため、マクロ系の状態が多様であって、実際にはマクロ系がどの量子状態にあるのかわからない(統計力学と同じ事情)ので、マクロ系の状態を確率的に考えざるを得ないからである。Sの解は常に一意的だから、その確率は‘見かけの確率’であって本質的なものではない。例えば、Sの猫(シュレーディンガーの猫)の場合、箱の中の猫は死んでいるか生きているかのどちらかが箱を開ける前にすでに決定しており、猫の状態(微視的状態)によってα崩壊の有無が決まる。猫が放射性物質のα崩壊の有無の検出器なのではなく、逆に放射性物質が猫の生死の検出器なのである(『5.光子の位置 h13.11.11』参照)。それは箱の中だけで完結している。箱の中の系はSに従って変化し、その結果は一意的である。放射性物質の状態は、ψ(崩壊する)+ψ(崩壊しない)であり、猫のミクロスコピック(微視的)な状態の違いによって、猫の生死が決定される。猫の生死は、光子(γ線)の状態がψ(出た)+ψ(出ない)で一定である以上、猫自身のミクロスコピックな状態によって決まる。つまり、猫は生きているか死んでいるかのどちらかひとつの状態だけを取る。箱の外にいる人は実際には猫のミクロスコピックな状態がわからないから、見かけの確率を導入せざるを得ない。
シュレーディンガーの猫の場合 h16.2.2
半減期後の放射性元素の状態はψ(崩壊した)+ψ(崩壊しない)である。放射性元素の崩壊とγ線の放射とは1対1に対応するので、γ線の状態はψ(出た)+ψ(出ない)となる。ここまではミクロ粒子間の反応であり、S式で記述される。
ところが、γ線とガイガーカウンターの反応はガイガーカウンターがマクロすなわち数多くの素粒子から構成されているため、Bの原理に従って、ガイガーカウンターの状態はψ(γ線を検出した)か、ψ(γ線を検出しない)かのどちらかひとつの状態になる。しかもS式にも従うので、この変化は本質的に確率的なものではなく、もしも人間がガイガーカウンターを構成するすべての素粒子の状態を知り、S式を解けるとすれば、一意的・確定的にψ(γ線を検出した)かψ(γ線を検出しない)かのどちらかであることがわかるのである。
あとは、古典力学の連鎖反応で、ガイガーカウンターがγ線を検出したならば、毒ビンが割れて猫は死ぬことになり、反対にガイガーカウンターがγ線を検出しなければ毒ビンが割れず猫は生きている。つまり、いわゆる“波動関数の収縮”はガイガーカウンターのところで起こることになり、箱の中の猫は生きているか死んでいるかどちらかひとつの状態を取る。
観測問題について h16.2.3
観測問題とはボルンの原理をシュレーディンガー方程式に基づいて証明することである。
ところで、観測装置はポテンシャルエネルギーV(r、t)として、観測される素粒子についてのシュレーディンガー方程式
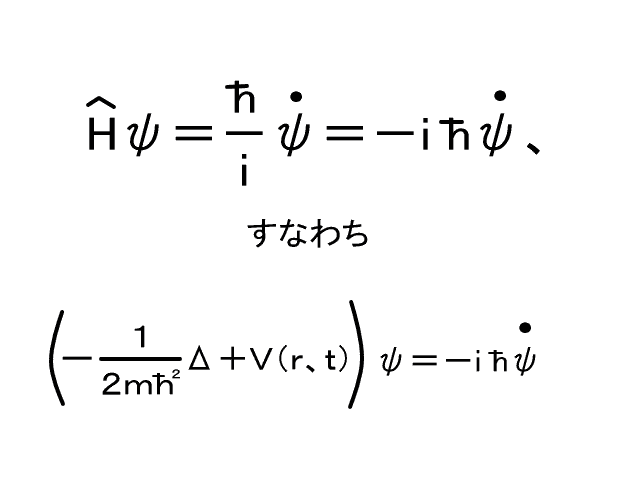
として表される。だから、これを解けばよい。
ところが、これは観測装置の具体的な構造を知らないかぎり解けないし、たとえ知ったとしても複雑すぎて解けない方程式なのである。(ここから先は、どうすればよいのだろう?…)
量子力学における量の概念 h16.3.1
距離は実在によって決められるものではなく、人間が定義する(決める)ものである。
距離が‘一意的に決まり’さえすれば、どう定義しても良いのだ。
これがリーマンの発想。古典力学の発想。
でも、量子力学はそうでない。
たとえ距離が一意的に決まらなくても、“確率的に決まり”さえすればよいのだ。
確率とは、量の概念の拡張だ。
例えば、‘さいころの目’の量が、一意的ではなくて、6意的であって、いろいろある。それを‘ひとつの量’と考えるわけだ。
でも、S式は一意的な結果を与える。
古典力学においても、さいころの運動は一意的であるはずだ。初期条件を確定すれば、運動方程式によって結果はひとつしかない。
確率的な量など実際には存在しない。
しょせん確率は‘人間が便宜的に定義した量’にすぎない。眼先の量にすぎない。でも、確率という量を定義すれば、たしかにわかることがある(例えば、2個のさいころを投げるとき、和が7の目が出ることが和が6の目の出ることよりも起こりやすい)から、考える価値はある。
相対論と量子力学(チャットより抜粋) h16.3.3
相対論では、『現象=実体×時空間』。つまり、実体が同じでも、それを見る座標系が違うと現象も違って見える。例えば、電荷に対し真っ直ぐな座標系から見ると電場だけしか現れないが、電荷に対し歪んだ座標系から見ると電場のほかに磁場が現れる。だから、電場と磁場は本質的に一体なのだ。同じ実体でも、それを見る座標系が違うと違う現象になるってとこがミソ。つまり、見られるもの(実体)が同じでも見るもの(座標系)が違えば見え方(現象)も違うってこと。実体しか考えない物理学野郎にはとうていわからないことだね。
量子力学でもそんなことあったねえ。量子力学においても、『現象=実体×観測系』。つまり、実体関数Ψについて違う物理量Aを観測すれば違った状態αになるってこと。この構造は相対論でも量子力学でも同じだ。人間にとって、実体そのものは見えず、見えるのは現象だけだから、相対論の構図を当てはめたくなる。でも、観測系は結局は物質なのだから、相対論のような座標系とは違うよね。観測系は物質なのだから、物と物との相互作用ってことになる。それはシュレーディンガー方程式で書けるだろう。観測問題についても、いろんなこと言っているけど、観測装置はあるひとつの物理量を測定するように作られているので、たとえ人間がいなくても、その装置だけで観測する物理量が決まるから、その装置のところで波動関数の収縮が起こるはずだ。装置は素粒子でできているからS式(シュレディンガー方程式)で記述できるし、結果は一意的になる。当たり前じゃないすか。
おまけ)それにしても、光は不思議な物質だ。光速度不変の原理からは相対性理論が生まれ、光のエネルギーの不連続性からは量子力学が生まれた。現代物理にとっては、まさに『はじめに光ありき。』だ。
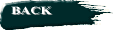
|