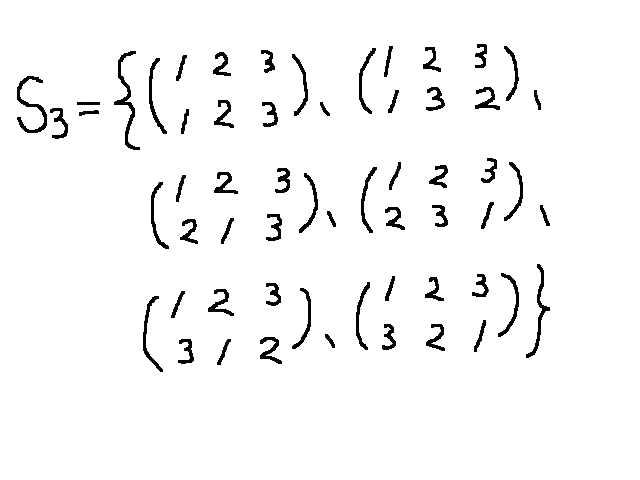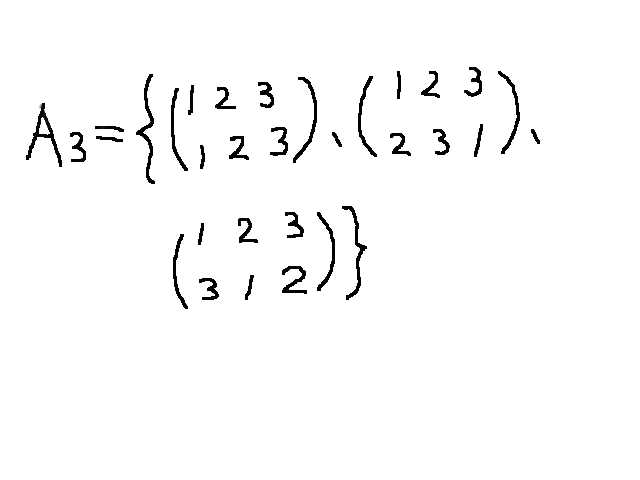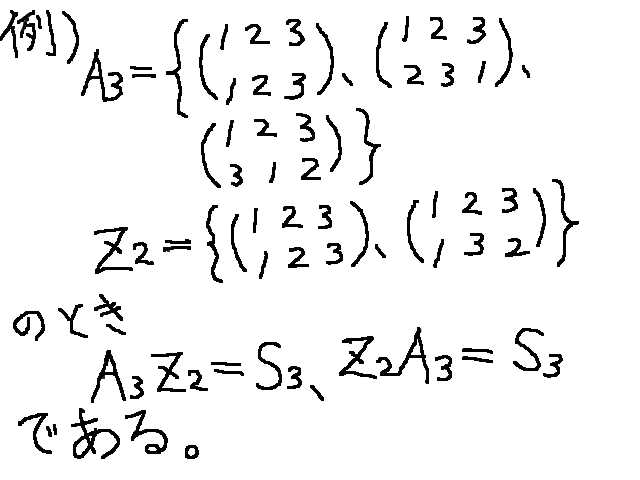|
孮榑偲僈儘傾棟榑

侾丏孮榑偺婎慴
丂俀丏僈儘傾棟榑
侾丏孮榑偺婎慴
亂傑偲傔亃
丂丒孮偲偼妡偗嶼偱寢傃偮偄偨尦偺乪孮傟乫偱偁傞丅
丂丒尦偺妡偗嶼傪孮偺妡偗嶼偵奼挘偡傞丅乮倎倐仺俙俛乯
丂
乵侾乶孮偺掕媊
丂侾乯孮偲偼丄尦偑妡偗嶼偲妱傝嶼偵偮偄偰暵偠偰偄傞乪廤崌乫偱偁傞丅
丂丂椺乯俽俁乮俁師懳徧孮乯
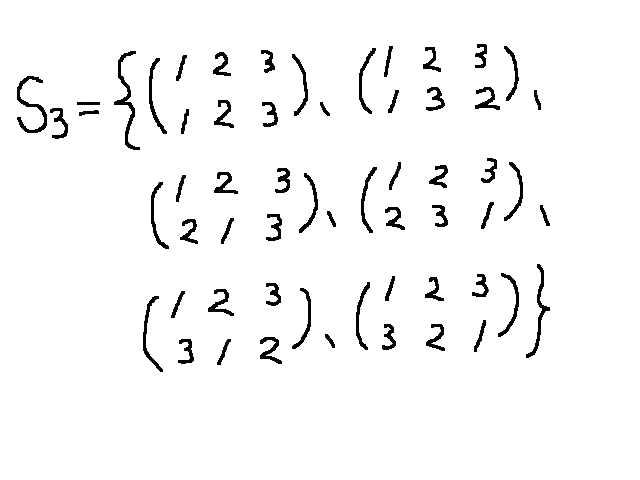
丂丂俽俁偺偳偺傆偨偮偺尦偺愊傕俽俁偵擖傝丄
丂丂丂丂丂丂偳偺尦偺媡尦傕丂丂丂丂俽俁偵擖傞丅
丂俀乯晹暘孮偲偼丄孲偺晹暘廤崌偑丄傑偨孮偵側偭偰偄傞傕偺偱偁傞丅
丂丂椺乯俙俁乮俁師岎戙孮乯偼俽俁偺晹暘孮偱偁傞丅丂
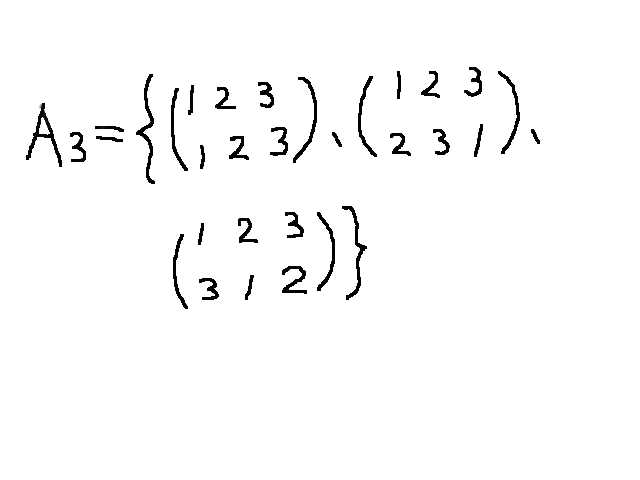
丂丂俙俁伡俽俁丄
丂丂俙俁偺偳偺傆偨偮偺尦偺愊傕俙俁偵擖傝丄
丂丂丂丂丂丂偳偺尦偺媡尦傕丂丂丂丂俙俁偵擖傞丅
乵俀乶孮偺愊乮妡偗嶼乯
丂丂俙偲俛傪孮偲偡傞丅
丂丂孮偺愊俙俛偲偼丄俙偺尦倎偲俛偺尦倐傪偙偺弴偵偐偗崌傢偣偨愊倎倐偺
丂丂偡傋偰偐傜側傞乪廤崌乫偱偁傞丅
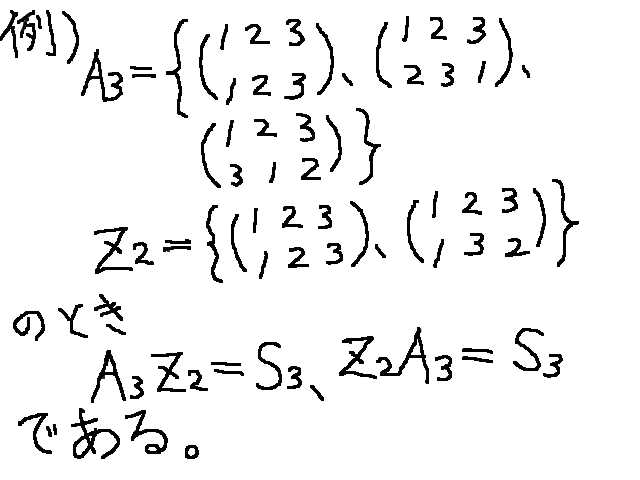
乵俁乶孮偺彜乮妱傝嶼乯
丂丂丂 俧傪孮丄俶傪俧偺惓婯晹暘孮乮掕媊偼懠偺杮傪嶲徠乯偲偡傞丅
丂丂丂孮偺彜俧乛俶偲偼丄暘巕偺孮俧傪暘曣偺孮俶偱傑偝偟偔乪妱傞乫偙偲丄偡側傢偪
丂丂丂俧乛俶亖俫偮傑傝俧亐俶亖俫偺偲偒丄俧亖俫俶偲側傞孮俫偺偙偲偱偁傞丅
丂丂丂惓婯晹暘孮偲偼彜偑孮偵側傞晹暘孮偱偁傞丅丂
丂丂丂椺乯俽俁丄俙俁丄倅俀乮俀師弰夞孮乯偺偲偒丄
丂丂丂丂丂俽俁乛俙俁亖倅俀丄偮傑傝俽俁亐俙俁亖倅俀
丂丂丂丂丂俽俁乛倅俀亖俙俁丄偮傑傝俽俁亐倅俀亖俙俁
丂丂曗侾乯堦斒偵偼丄孮亐晹暘孮亖廤崌乮孮偱偼側偄乯偱偁偭偰丄
丂丂丂丂丂偲偔偵晹暘孮偑惓婯晹暘孮偺偲偒
丂丂丂丂丂孮亐惓婯晹暘孮亖晹暘孮偲側傞丅
丂丂丂丂丂乮偨偩偟丄偄偮偱傕彜偼嵟彫僒僀僘乮尦偺屄悢偑嵟彫乯偺廤崌偵側傞傛偆偵偲傞丅乯
丂丂丂丂丂惓婯晹暘孮偲偼丄惍悢偵偍偗傞乪栺悢乫偺傛偆側傕偺偱偁傞丅
丂丂曗俀乯俧偑孮偱俶偑俧偺惓婯晹暘孮偺偲偒偵偼
丂丂丂丂丂俧乛俶亖俶乢俧亖俫側偺偱丄偨傫偵俧亐俶亖俫偱傛偄丅
丂丂丂丂丂堦斒偵偼丄尦偺愊偑壜姺偲偼尷傜側偄偺偱
丂丂丂丂丂俧乛俶亗俶乢俧偱偁傞丅
乵係乶摨宆掕棟乮尰戙悢妛偼廤崌偲懳墳偱峫偊偰偄偗偽偄偄乯
丂丂侾乯弨摨宆掕棟
丂丂丂丂孮G偲孮G'偺娫偵弨摨宆幨憸f乮孮偵偍偗傞弨摨宆幨憸偲偼丄
丂丂丂丂愊傪曐偮幨憸偡側傢偪倖乮倶倷乯亖倖乮倶乯倖乮倷乯乯偑偁傞偲偒丄
丂丂丂丂孮G乫偺扨埵尦e'偵幨傞孮G偺廤崌N偼孮G偺惓婯晹暘孮偱偁偭偰丄
丂丂丂丂G/N偲G'偺懳墳偼堦懳堦偺弨摨宆幨憸偡側傢偪摨宆幨憸偲側傞丅
丂丂丂丂偮傑傝丄俧乛俶乣俧乫丄偡側傢偪丂
丂丂丂丂孮俧傪妀俶乮偠偮偼俧偺惓婯晹暘孮偵側傞乯偱妱偭偨摎偊偲偟偰偺孮偲丄
丂丂丂丂孮俧乫偡側傢偪俧乫乛倕乫乮倕乫偼扨埵尦偩偗偐傜側傞廤崌乯偲偑摨宆偵側傞丅
丂丂丂丂摨宆偲偼丄
丂丂丂丂鶣乯廤崌偲偟偰尦偺悢偑摨偠丂
丂丂丂丂鶤乯戙悢偲偟偰愊偺娭學偑摨偠
丂丂丂丂偙偲偱偁傞丅
丂丂俀乯戞堦摨宆掕棟乮弨摨宆掕棟偺堦斒壔乯
丂丂丂丂孮G'偺惓婯晹暘孮N'偵幨傞孮G偺廤崌N偼孮G偺惓婯晹暘孮偱偁偭偰丄丂丂丂丂
丂丂丂丂俧乛俶乣俧乫乛俶乫丄偡側傢偪
丂丂丂丂彜俧乛俶偮傑傝俧亐俶偲偄偆妱傝嶼偺寢壥偲偟偰偺傂偲偮偺孮偲
丂丂丂丂彜俧乫乛俶乫偮傑傝俧乫亐俶乫偲偄偆妱傝嶼偺寢壥偲偟偰偺傂偲偮偺孮偲偑
丂丂丂丂摨宆偵側傞丅
丂丂俁乯戞擇摨宆掕棟乮壜栺棩乯
丂丂丂俫俶乛俶亖俫乛俫伩俶丂乮俫偼俧偺晹暘孮丄俶偼俧偺惓婯晹暘孮乯
丂丂丂嵍曈俫俶乛俶偮傑傝俫偐偗傞俶傢傞俶偲偄偆寁嶼傪峴偭偨寢壥摼傜傟偨傂偲偮偺孮偲丄
丂丂丂塃曈俫乛俫伩俶偮傑傝俫傢傞乮俫伩俶乯偲偄偆寁嶼傪峴偭偰摼傜傟偨摎偊偺孮偑丄
丂丂丂摨宆偮傑傝廤崌揑丄戙悢揑偵摨偠偵尒偊傞偙偲丅
丂丂丂曗侾乯晛捠偺悢偺応崌偵偼
丂丂丂丂丂嵍曈俫俶乛俶偼丄暘曣偲暘巕傪乪栺暘乫偟偰
丂丂丂丂丂俫俶乛俶亖俫偲側傞偑丄孮偺寁嶼偱偼俫傗俶偼
丂丂丂丂丂乪傂偲偮偺悢乫偱偼側偔乪廤崌乫側偺偱丄
丂丂丂丂丂俫俶乛俶亗俫偲側傞丅
丂丂丂丂丂偨偲偊偽丄偲偔偵俫亖俶乮亗侾乯偲偟偰丄
丂丂丂丂丂俫俶乛俶亖俶俶乛俶亖俶乛俶亖侾亗俫偲側傞丅
乵俆乶孮偺扨弮孮暘夝
丂丂扨弮孮偲偼丄侾偲偦傟帺恎埲奜偺惓婯晹暘孮傪帩偨側偄孮偱偁傞丅扨弮孮偲偼丄惍悢偵偍偗傞乪慺悢乫偺傛偆側傕偺偱偁傞丅
丂丂桳尷孮偼偮偹偵扨弮孮偺愊偵暘夝偝傟傞丅惍悢偑慺悢偺愊偵暘夝偝傟傞偺偲摨條偱偁傞丅
丂丂椺乯俽俀乮俀師懳徧孮乯亖倅俀乮俀師弰夞孮乯
丂丂丂丂俽俁乮俁師懳徧孮乯亖倅俀倅俁
丂丂丂丂俽係乮係師懳徧孮乯亖倅俀倅俁倅俀'倅俀"
丂丂丂丂俽俆乮俆師懳徧孮乯亖倅俀俙俆乮俙俆偼扨弮孮乯
丂丂丂丂丂俙俆偼乪暋嶨側乫孮側偺偱丄亀俆師曽掱幃偼儀僉崻偩偗偱偼夝偗側偄丅亁
俀丏僈儘傾棟榑
戙悢曽掱幃偺旕壜夝惈偼丄侾師丄俀師丄俁師丄係師側偳偺嬶懱揑曽掱幃偵偮偄偰偺夝朄偺僾儘僙僗傪暘愅偟丄堦斒壔偡傟偽尒偊偰偔傞丅椺偊偽丄俁師曽掱幃偺夝朄偼丄杮俀乮壓傪尒傛乯偺侾俁係儁乕僕偵丄係師曽掱幃偺夝朄偼丄杮俀偺侾俁俇儁乕僕偵傢偐傝傗偡偔彂偄偰偁傞丅
仧嶲峫偵偟偨杮乮偳偪傜傕僋儘僱僐儎儅僩偺戭攝曋偱攦偭偨乯
侾乯乽弶傔偰妛傇恖偺偨傔偺孮榑擖栧乿墶揷堦榊挊丄尰戙悢妛幮丄俀俇侽侽墌乮惻暿乯
俀乯乽僈儘傾棟榑島媊乿懌棫峆梇挊丄擔杮昡榑幮丄俀俋侽侽墌乮惻暿乯
偁傞曽掱幃偑夝偗傞偲偼丄曽掱幃偺夝X偑丄
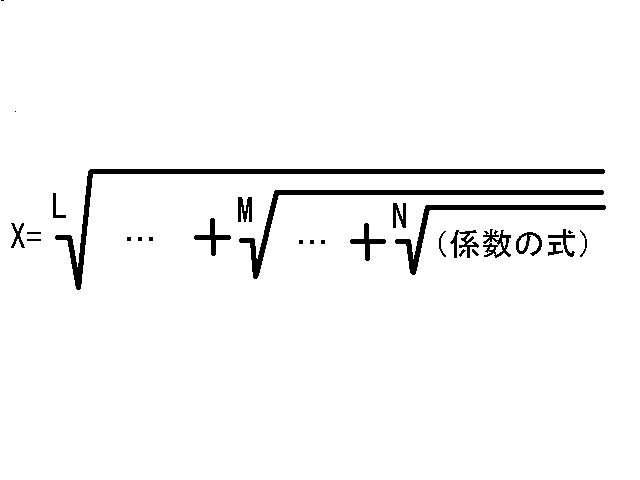
偺宍偵彂偗傞偙偲偱偁傞丅
偟偨偑偭偰丄曽掱幃偑夝偗側偄偙偲傪帵偡偵偼丄夝X偑忋偺宍偵彂偗側偄偙偲傪帵偣偽傛偄丅
曽掱幃偑夝偗側偄偙偲偼丄
乷P乥P偼偁傞曽掱幃偺夝丄偍傛傃偦傟傜偺壛尭忔彍乸偑
乷Q乥Q偼偁傞曽掱幃偺學悢偵壛尭忔彍偲傋偒忔崻傪巤偟偨傕偺乸偵
娷傑傟側偄偙偲傪帵偣偽傛偄丅
偦偙偱忋偺傆偨偮偺廤崌偺乪懳徧惈乫偑堎側傞偙偲傪丄乪懳徧惈乫偺堄枴傪榑棟揑偵尩枾偵掕媊偡傞偙偲偵傛偭偰帵偣偽傛偄丅乪懳徧惈乫偲偼丄偄傢偽偦偺廤崌偺乪宍乫偱偁傝丄偦傟偼僈儘傾孮偱昞偝傟傞丅
僈儘傾孮偲偼丄廤崌偐傜摨偠廤崌傊偺帺屓摨宆幨憸偺孮偱偁傞丅
偙偙偱偺廤崌乮偄傢備傞懱乯偵偍偗傞帺屓摨宆幨憸偲偼丄榓偲愊傪曐偮幨憸丄
偡側傢偪倖乮倶亄倷乯亖倖乮倶乯亄倖乮倷乯丄倖乮倶倷乯亖倖乮倶乯倖乮倷乯丅
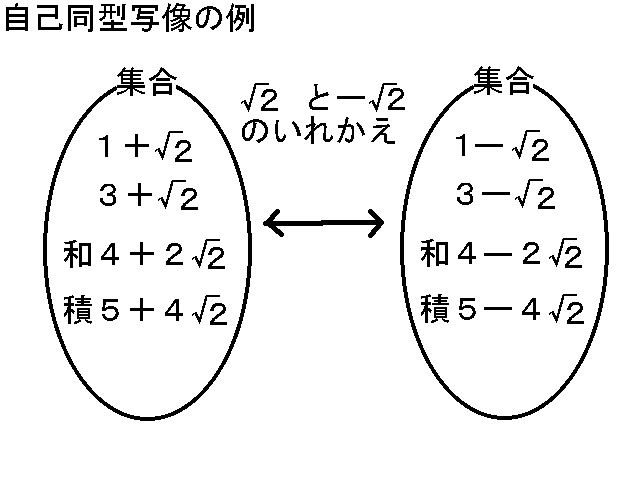
嵍偺廤崌乷P乸偺帺屓摨宆幨憸偼(堦斒偵)夝偺偄傟偐偊偱偁傝丄塃偺廤崌乷Q乸偺帺屓摨宆幨憸偼侾偺傋偒忔崻傪偐偗傞偙偲偱偁傞丅
偟偨偑偭偰丄嵍偺廤崌偺乪懳徧惈乫偼(堦斒偵)Sn(値師懳徧孮)偱偁傝丄塃偺廤崌偺乪懳徧惈乫偼Zm(m師墌孮)偺愊偱偁傞丅
塃偺廤崌偱偼丄奺抜奒偑撈棫偵側傞偺偱丄侾抜奒偛偲偵暘愅偟偰尒偰偄偔偲丄Zm偺愊偵側傞偙偲偑傢偐傞丅
偄傢偽丄廤崌偺乪宍乫偑丄嵍偺廤崌偱偼惓懡柺懱揑偱偁傞偺偵偨偄偟丄塃偺廤崌偱偼墌揑偱偁傝丄傆偨偮偺廤崌偼乪宍偑堘偭偰偄傞乫偺偱偁傞丅
嵍偺廤崌乷P乸偑塃偺廤崌乷Q乸 偵娷傑傟側偄偙偲傪帵偡偵偼丄Sn偑Zr偺愊偵彂偗側偄偙偲傪偄偊偽偄偄[徻偟偔偼丄懠偺悢妛彂傪嶲徠]丅
椺偊偽丄S5偼Zm偺愊偺宍偵彂偗側偄偐傜丄堦斒偺俆師曽掱幃偼夝偗側偄偙偲偵側傞丅
栠傞
|