実在の世界には眼で見える坂道のほかに、電磁空間という眼で見えない坂がある。
電位Vは‘見えない坂’の高さのようなものである。
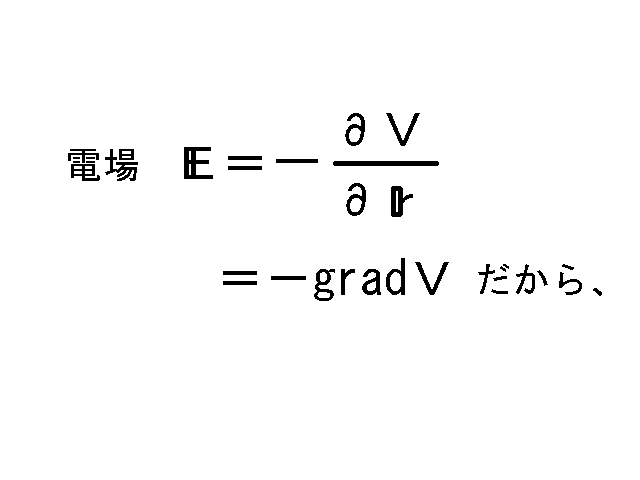
電場とは‘見えない坂’の勾配(傾き)のようなものだ。
(私は学生時代、電磁気を弾性体に喩えて電場Eを変位のように考えて、チンプンカンプンでした。そう考えると、荷電粒子の周りの電磁場に穴が開いたみたいになってうまくいかない。)
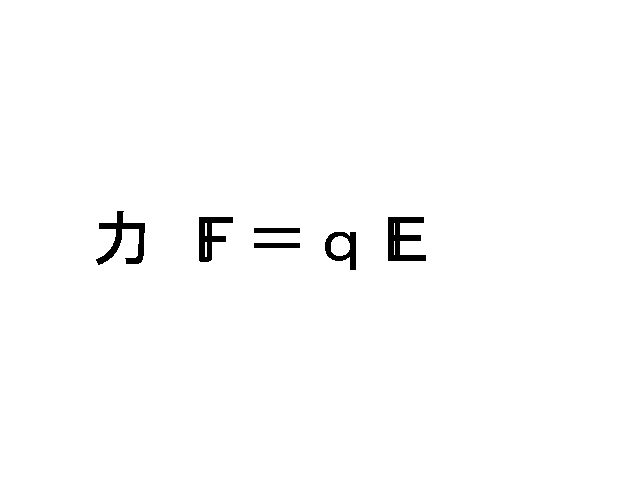
ついでに、電荷qは‘見えない坂’の上ではたらく質量(重量)のようなものだ。
見えない坂 h15.8.16
実在の世界には眼で見える坂道のほかに、電磁空間という眼で見えない坂がある。
電位Vは‘見えない坂’の高さのようなものである。
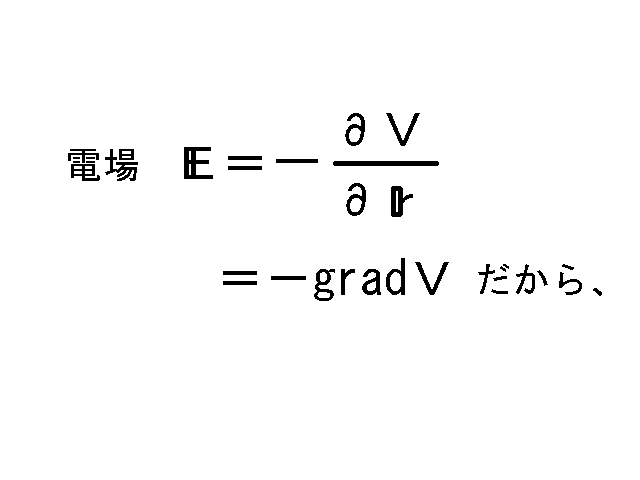
電場とは‘見えない坂’の勾配(傾き)のようなものだ。
(私は学生時代、電磁気を弾性体に喩えて電場Eを変位のように考えて、チンプンカンプンでした。そう考えると、荷電粒子の周りの電磁場に穴が開いたみたいになってうまくいかない。)
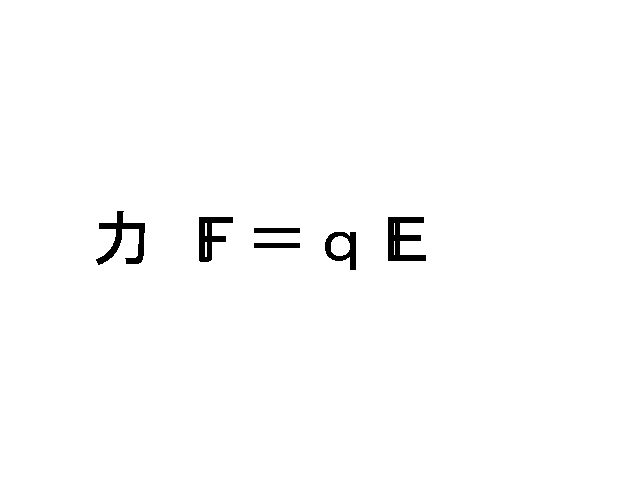
ついでに、電荷qは‘見えない坂’の上ではたらく質量(重量)のようなものだ。
車はどうして前に進むのか? h15.8.16
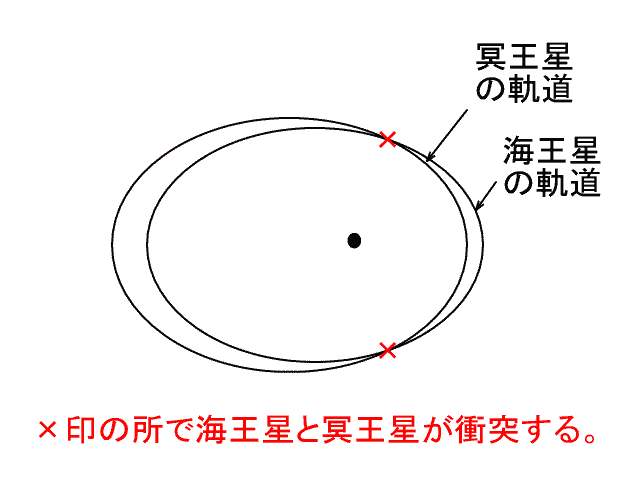
自動車はタイヤで地面と接している。
接地点において、タイヤが地面を後ろに押す。
ニュートンの運動の第3原理(作用・反作用の法則)により、タイヤが地面を後ろに押すと、逆に地面がタイヤを前に押すことになる。
この力で車は前に動くのだ。(おわり)
衝突する惑星 h16.5.30
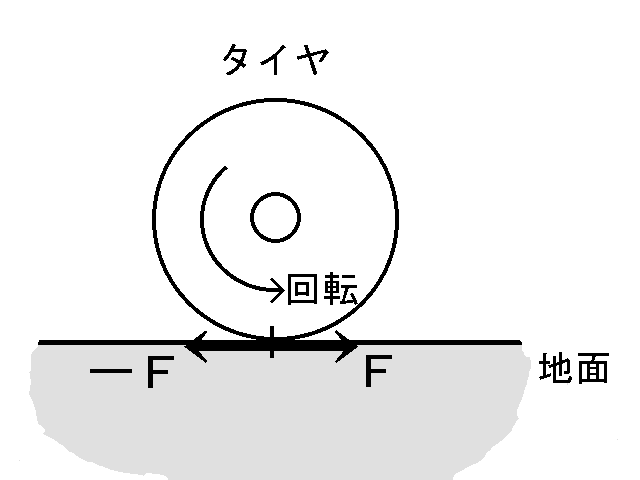
太陽系の各惑星は太陽を中心とする楕円軌道を描いている。
ところで、海王星と冥王星とは軌道が交差し、その周期が互いに素だから、
いつかは海王星と冥王星は衝突する。
熱力学
比重とエントロピー h16.8.26
比重とは物体の重さを体積で割ったものだ。
同様に、エントロピーとは物体の熱を温度で割ったものだ。〔比熱となにが違うのか?〕
天才といっても、その程度のものだ。〔同じように、知覚における時空間と五感における時空間との違い(差、割り算)から‘感覚’と‘実在’の概念が出来る。ひとたび概念が作られれば、多くのことがわかるようになる。〕
エントロピーとは何か? h21.8.12
多体系には一個の粒子にはなかった“新しい量”が現れる。
それがエントロピーだ。
多体系を捉えるには、“多体系に相応[ふさわ]しい量”を考えねばならない。
それがエントロピーだ。
『一個の粒子』について位置とか運動量を考えるように、
『多体系』については、圧力とか体積とかエネルギーとかエントロピーを考えるのだ。[そもそも“物の名前”も人間が実在を捉えるために考え出した概念であるといえる。人類は、大昔からなんとかして実在の世界を理解しようと努[つと]めてきたのだ。]
そうすれば、多体系については一意的に状態を定義できるのである。
一個の粒子が同じであるとは、位置と運動量が同じであることだが、
一個の多体系が同じであるとは、体積とエネルギーとエントロピーが同じであることだ。[詳しいことは忘れた。]
つまり、多体系には“微視的状態の数”という量がある。
それを考慮に入れないと多体系のことはわからないということである。
多体系は、同じ条件のもとで、『微視的状態の数が最大の状態を取る』のが自然であると考えられる。
つまり、統計力学や熱力学では時間のことは考えないのだ。運動のことは考えないのだ。
多体系については1個の粒子の場合とは捉[とら]え方が違うのだ。
統計力学や熱力学では、運動量の代わりにエントロピーすなわち微視的状態の数があるといってもいい。[S=klogW。]
1個の粒子では、時間と位置と運動量で対象を捉えるが、
多体系では、体積とエネルギーとエントロピー=微視的状態の数で対象を捉えるのだ。
1個の粒子では、『運動量の時間変化が力である』ことを使って1個の粒子の取る状態を求めるが、
多体系では、『エントロピーが最大である』ことを使って多体系の取る状態(平衡状態)を求めるのだ。[デカルトが運動量の概念を考え出し、ニュートンが運動量の方程式を作ったように、カルノーがエントロピーーの概念を考え出して、クラウジウスがエントロピー最大の法則を作ったのだ。]
つまり、多体系は、どのような初期条件からでも遅かれ早かれ同一の平衡状態に達し、あとは平衡状態の周りで小さく振動し続けているのである。
多体系の時間的変化を考えると面倒臭くなるので、省略して考えているのである。“それでわかることを考えよう”というのが、[平衡系の]熱・統計力学である。食べ物の味は不味くても栄養さえ足りていれば人間は生きていけると考えて、食べ物の味を省略するのと同じことである。[つまり、本当は多体系は時間とともに運動(変化)するからS=S(t)なのだが、それを計算するのは面倒(不可能)なので、S=S(t=∞)=Smaxとなる平衡状態についてだけ考えるのである。実際には多体系は運動している。例えば、窓ガラスは液体だから、作ったときには平べったいが、時間が経つと重力で引かれて下のほうが厚くなって上の方が薄くなるのである。]
多体系の時間的変化についての研究はこれからの課題である。
エントロピーとは何か?(その2) h21.8.16
多体系のエントロピーが大きい状態が出現しやすいのは、多体系の状態についてのミクロな分類とマクロな分類との違いによる錯覚である。昔の人は多体系のマクロな分類だけを考えていたから、エントロピーの意味がわからなかったのである。しかし、実際には、ひとつのマクロな状態にはミクロな状態がたくさん対応するから、ひとつのミクロな状態がどれも同じ確率で現れるとすれば、ミクロな状態がたくさんあるマクロな状態が出現しやすいのである。
例えば、真空の中で気体が膨張する場合、すべての気体分子を包む最小の滑らかな曲面を考えれば気体の“体積”が定義できる。気体は外からエネルギー(力学的エネルギーや熱エネルギー)をもらわなくても、自分ひとりで状態が変化できる。エネルギーのことだけしか考えなければ、気体は膨張する前の状態と膨張した後の状態を自由に行き来できるはずである。ところで、膨張する前の状態と膨張した後の状態では、膨張した後の状態のほうが膨張する前の状態よりもミクロな状態を多く含むから[膨張する前も膨張した後もともにミクロな状態を無限個含むけれども、∞/∞の比を考えれば比は有限であって、膨張した後のほうが膨張する前よりもミクロな状態を多く含むことがわかる。]、『ミクロな状態の出現する頻度が同じである』とすれば、膨張した後のマクロな状態のほうが膨張する前のマクロな状態よりも現れやすいのである。その結果、気体の体積が増える向きに変化する。つまり、『多体系のミクロな状態が同じ確率で現れるために、多体系のマクロな状態がエントロピーの増える向きに変化する』のである。
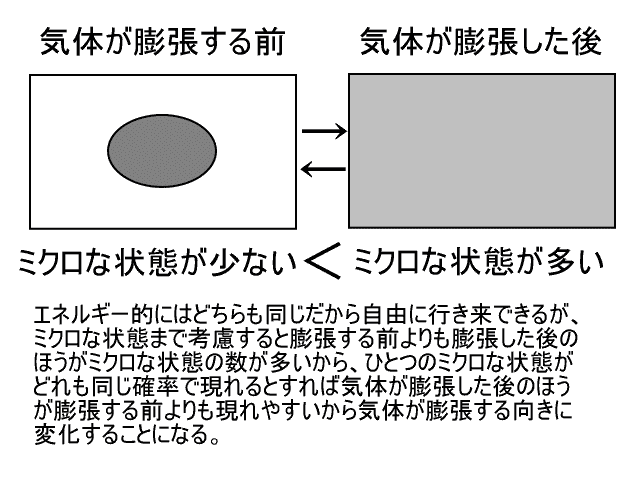
人間には多体系(例、気体)のマクロな状態しか区別できずミクロな状態が区別できない錯覚によって、多体系はエントロピーが増える方向に変化するように人間の眼には見えるのである。
例えば、膨張する前のミクロな状態が10個で、膨張した後のミクロな状態が1000個だとしたとき、両方の絵を混ぜてパラパラマンガにしたとき、人間の眼には膨張した後の状態ばかりが見えるのである。だから、多体系はミクロな状態の数が一番多い状態つまりエントロピーが最大の状態を取るのである。
医学
どうして人間は癌[がん]にかかるのか? h24.9.6
人間が年をとると癌にかかるのは、免疫能が落ちているからである。
免疫細胞が癌細胞を排除できないから癌にかかるのである。
癌細胞に何かをくっつけて、免疫細胞が癌細胞を認識できるようにすればいい。